Importance of RMS value in electrical system

In Alternating Current (AC) system magnitude of electrical quantities are expressed in root mean square (rms) values. 

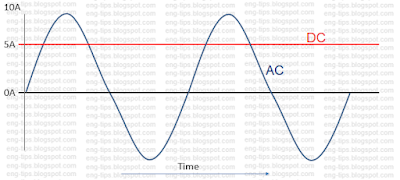
In Direct Current (DC) system, magnitude of current or voltage is constant over the period of time. We can specify that 5A current is flowing or 12V potential difference is existing between two points. For example, DC 5A is shown below, Red being positive and black being negative. In this image, one AC signal is also shown in Blue colour.

The question is: at which point we should specify the current as it is continuously varying and changing its sign from +ve to -ve and -ve to +ve in each cycle. One of the approach may be specifying peak value:

The problem with peak value is that, in actual, it appears for a fraction of time in a cycle (two time in a cycle, one in +ve and another in -ve). for rest of the cycle, magnitude is less than peak value. If we compoare 5A DC and 5A AC (peak value), DC current will have more power over a period of time. That is how concept of RMS value came. It is value of AC signal, for which same value DC signal dissipates the same power in a resistor. 

That means heat produced by 5A DC over a period of time "T" and by 5A AC over time "T" shall be same. Therefore, power of both AC and DC signals is same.

For understanding rms value, let us calculate actual energy dissipated in heat for one cycle of AC. First divide AC cycle in "n" parts on time scale. Calculate energy of each part by formula I²Rt and add them up over the period of one cycle.  

In above image energy for one cycle will be I₁²Rt₁ + I₂²Rt₂ + I₃²Rt₃ +…e I_n²Rt_n 

Energy (over one cycle) E = (I₁²Rt₁ + I₂²Rt₂ + I₃²Rt₃ +…. I_n²Rt_n)

In the above equation t₁ =t₂ =t₃ …=t_n =t

Energy (over one cycle) = (I₁² + I₂² + I₃² +…. I_n²) Rt

Average energy for n^th part

Energy (for n^th part) = (I₁² + I₂² + I₃² +…. I_n²) Rt /n

Power (for n^th part) = E/t = (I₁² + I₂² + I₃² +…. I_n²) R /n        …EQ1

As we know Power P = I²R                                                    …EQ2

From EQ1 and EQ2:

I²R = (I₁² + I₂² + I₃² +…. I_n²) R /n

I² = (I₁² + I₂² + I₃² +…. I_n²)/n

I =  √ {(I₁² + I₂² + I₃² +…. I_n²)/n}

Therefore, RMS value is is the square root of the arithmetic mean of the squares of the values.

In AC system values mentioned are always rms values unless otherwise specified. For exmple in AC system:

• 200V means 200V RMS value
• 10A means 10A RMS value
• 200Vpeak means 200V peak value
• 10Apeak means 10A peak value

RMS value for common waveforms is as below:

• Sine wave: RMS value = Peak value / √2
• Square wave: RMS value = Peak value
• Saw tooth wave / triangle wave: RMS value = Peak value / √3

Peak value is significant for insulation calculations,

What if CT secondary is open circuit?

CT secondary shall always be kept short circuited. What happens if CT is open circuit?

Current Transformer (CT) is an instrument transformer used to reduce or mutiply current by a pre-defined factor. 

It has small number of primary turns and large number of secondary turns. Generally primary winding has only one turn, as primary conductor simply pass through CT core.  Secondary winding has large number of turns (may be 1000, depending on ratio). In the image below, only few turns are shown in CT secondary for simplicity . Primary winding and secondary winding are wound on magnetic core.

From the above, Primary current Ip flows through primary winding. Due to this current magnetic field is developed and magnetic flux φ flows in the core. This alternating flux produces voltage Vs in secondary winding. Normally, Zs is very low (or may be short circuit),  this voltage develops current Is in secondary winding. 

According to Lenz's law:

The current induced in a circuit due to a change in a magnetic field is directed to oppose the change in flux and to exert a mechanical force which opposes the motion.

Therefore, flux produced by secondary current is opposite to flux produced by primary winding. Theroritically, both flux should be same but in oppsite direction. However, in actual, there will be a very small difference due to leakage flux. The resultant flux, difference of flux produced by primary current and flux produced by secondary current, is very small for normal load current. It magnifies in case of higher fault current. CT core is designed to carry resultant flux upto a certain fault level. 

For low value of Zs, CT can be considered as short circuited transformer. Reactance of primary winding will be very small, hence very low voltage drop across primary terminals.

If CT is open circuit, there will be no secondary current and no flux produced by secondary current. Magnetic core will get saturated by high amount of flux produced by primary current. 

In saturated part of waveform there will be no change in flux and due this there will be no e.m.f. induced in secondary. This will result in no current in secondary.

As CT is already staurated in this case, voltgae developed will not be sinusoidal. It will contain harmonics and wave shape will be spiky. The peak value of voltage will be very high in the range of 2-3kV. This higher voltage is dangerous for persons working in panels and equipment. This high voltage can lead to failure of insulation in CT, Cables, relays, terminal blocks etc.