Importance of RMS value in electrical system

In Alternating Current (AC) system magnitude of electrical quantities are expressed in root mean square (rms) values. 

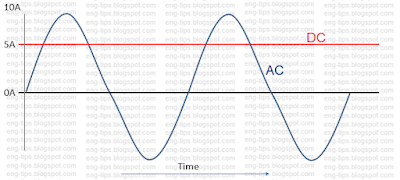
In Direct Current (DC) system, magnitude of current or voltage is constant over the period of time. We can specify that 5A current is flowing or 12V potential difference is existing between two points. For example, DC 5A is shown below, Red being positive and black being negative. In this image, one AC signal is also shown in Blue colour.

The question is: at which point we should specify the current as it is continuously varying and changing its sign from +ve to -ve and -ve to +ve in each cycle. One of the approach may be specifying peak value:

The problem with peak value is that, in actual, it appears for a fraction of time in a cycle (two time in a cycle, one in +ve and another in -ve). for rest of the cycle, magnitude is less than peak value. If we compoare 5A DC and 5A AC (peak value), DC current will have more power over a period of time. That is how concept of RMS value came. It is value of AC signal, for which same value DC signal dissipates the same power in a resistor. 

That means heat produced by 5A DC over a period of time "T" and by 5A AC over time "T" shall be same. Therefore, power of both AC and DC signals is same.

For understanding rms value, let us calculate actual energy dissipated in heat for one cycle of AC. First divide AC cycle in "n" parts on time scale. Calculate energy of each part by formula I²Rt and add them up over the period of one cycle.  

In above image energy for one cycle will be I₁²Rt₁ + I₂²Rt₂ + I₃²Rt₃ +…e I_n²Rt_n 

Energy (over one cycle) E = (I₁²Rt₁ + I₂²Rt₂ + I₃²Rt₃ +…. I_n²Rt_n)

In the above equation t₁ =t₂ =t₃ …=t_n =t

Energy (over one cycle) = (I₁² + I₂² + I₃² +…. I_n²) Rt

Average energy for n^th part

Energy (for n^th part) = (I₁² + I₂² + I₃² +…. I_n²) Rt /n

Power (for n^th part) = E/t = (I₁² + I₂² + I₃² +…. I_n²) R /n        …EQ1

As we know Power P = I²R                                                    …EQ2

From EQ1 and EQ2:

I²R = (I₁² + I₂² + I₃² +…. I_n²) R /n

I² = (I₁² + I₂² + I₃² +…. I_n²)/n

I =  √ {(I₁² + I₂² + I₃² +…. I_n²)/n}

Therefore, RMS value is is the square root of the arithmetic mean of the squares of the values.

In AC system values mentioned are always rms values unless otherwise specified. For exmple in AC system:

• 200V means 200V RMS value
• 10A means 10A RMS value
• 200Vpeak means 200V peak value
• 10Apeak means 10A peak value

RMS value for common waveforms is as below:

• Sine wave: RMS value = Peak value / √2
• Square wave: RMS value = Peak value
• Saw tooth wave / triangle wave: RMS value = Peak value / √3

Peak value is significant for insulation calculations,